Compensation is the latest strategy some of my students have been exploring in class. This strategy requires students to have a complete understanding of place value and the number system. It is a little different for addition and subtraction, so I will break each section apart below.
Addition:
This strategy is based on maintaining the value of the whole. With addition, as long the whole is maintained the sum will be the same. Therefore, what ever is done to one addend, the opposite must be done to the other addend. Let's say that we are adding 36 + 45.
Step 1: Find the amount that can be added or subtracted from the addend (36) so that the digit in the ones place becomes a 0.
Step 2: Once you determine the number you are adding or subtracting from the addend (36), the opposite must be done to the addend (45).
Step 3: Find the sum of the two new numbers you created.
This probably sounds very confusing, so lets look at a picture for clarification.
Addition:
This strategy is based on maintaining the value of the whole. With addition, as long the whole is maintained the sum will be the same. Therefore, what ever is done to one addend, the opposite must be done to the other addend. Let's say that we are adding 36 + 45.
Step 1: Find the amount that can be added or subtracted from the addend (36) so that the digit in the ones place becomes a 0.
Step 2: Once you determine the number you are adding or subtracting from the addend (36), the opposite must be done to the addend (45).
Step 3: Find the sum of the two new numbers you created.
This probably sounds very confusing, so lets look at a picture for clarification.
Subtraction:
This strategy is based on the fact that subtraction is the distance between two numbers on the number line. As long as the distance is maintained, you can adjust the numbers to make an easier problem. Let's take a look at the problem 57-28.
Step 1: Find the amount that can be added or subtracted from the minuend (57) so that the digit in the ones place becomes a 9. (We want to eliminate any kind of regrouping.)
Step 2: Once you determine the number you are adding or subtracting from the minuend (57), you must add or subtract the same number from the subtrahend (28) to keep the distance the same on the number line.
Step 3: Find the difference between the two new numbers you created.
Again, let's break it down a little more. Take a look at the number line below:
Keep practicing your strategies. Remember your child will not be asked at any time to only use a certain strategy (like compensation) on any assessments or classwork. Students choose the strategy that works best for them on the problem they are working on.
This strategy is based on the fact that subtraction is the distance between two numbers on the number line. As long as the distance is maintained, you can adjust the numbers to make an easier problem. Let's take a look at the problem 57-28.
Step 1: Find the amount that can be added or subtracted from the minuend (57) so that the digit in the ones place becomes a 9. (We want to eliminate any kind of regrouping.)
Step 2: Once you determine the number you are adding or subtracting from the minuend (57), you must add or subtract the same number from the subtrahend (28) to keep the distance the same on the number line.
Step 3: Find the difference between the two new numbers you created.
Again, let's break it down a little more. Take a look at the number line below:
Keep practicing your strategies. Remember your child will not be asked at any time to only use a certain strategy (like compensation) on any assessments or classwork. Students choose the strategy that works best for them on the problem they are working on.
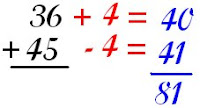
No comments:
Post a Comment